比特币的数学基础:揭秘加密货币的数学原理

比特币作为一种全球知名的加密货币,其背后有着复杂的数学原理。本文将深入探讨比特币的数学基础,帮助读者了解这一数字货币的运作机制。
区块链与哈希函数
区块链是比特币的核心技术之一,它是一种去中心化的分布式账本。在区块链中,每个区块都包含了一系列的交易数据,这些数据通过哈希函数进行加密处理。
哈希函数是一种将任意长度的数据映射为固定长度数据的函数。在比特币中,常用的哈希函数有SHA-256和RIPEMD-160。这些哈希函数具有以下特点:
单向性:给定输入数据,可以快速计算出哈希值,但无法从哈希值反推出原始数据。
抗碰撞性:在所有可能的输入数据中,找到两个具有相同哈希值的输入数据的概率极低。
抗篡改性:对原始数据进行任何微小的修改,都会导致哈希值发生巨大变化。
这些特性使得哈希函数在比特币的区块链技术中扮演着至关重要的角色。
工作量证明(Proof of Work,PoW)
比特币的挖矿过程实际上是一个工作量证明的过程。矿工需要通过解决复杂的数学问题来验证交易,并将新的区块添加到区块链上。
在比特币网络中,矿工需要找到满足特定条件的nonce值,这个值是随机生成的数字。当矿工找到这个nonce值时,会计算出区块的哈希值,并确保这个哈希值小于比特币协议中规定的目标值。
这个过程需要大量的计算能力,因此矿工通常会使用专门的挖矿设备(ASIC矿机)来进行计算。随着比特币网络的不断发展,挖矿难度会不断调整,以保持新区块生成的速度稳定。
椭圆曲线数字签名算法(ECDSA)

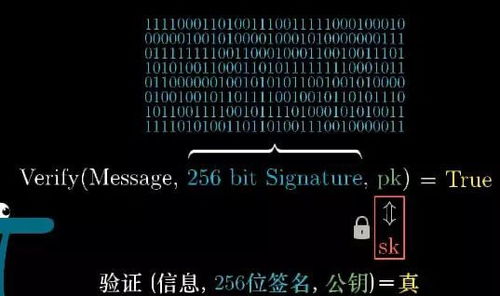
比特币使用椭圆曲线数字签名算法(ECDSA)来保证交易的安全性。ECDSA是一种基于椭圆曲线密码学的数字签名算法,它具有以下特点:
安全性:在当前的计算能力下,很难伪造或破解ECDSA签名。
效率:与传统的数字签名算法相比,ECDSA在保证安全性的同时,具有更高的计算效率。
在比特币交易中,用户需要使用私钥对交易进行签名,私钥是用户在比特币网络中的唯一身份标识。只有拥有对应公钥的用户才能验证并接收交易。
比特币的数学挑战与未来展望

尽管比特币的数学基础相对成熟,但仍然存在一些挑战和潜在的风险。
首先,随着量子计算的发展,现有的加密算法可能会受到威胁。如果量子计算机能够破解现有的加密算法,那么比特币的安全性将面临巨大挑战。
其次,比特币的挖矿过程消耗了大量的电力资源,这引发了关于可持续性的担忧。未来,比特币网络可能需要寻找更加节能的挖矿方式。
尽管存在这些挑战,比特币的数学基础仍然为其提供了强大的安全保障。随着技术的不断进步,相信比特币的数学原理将会得到进一步完善,为全球用户提供更加安全、可靠的数字货币服务。
